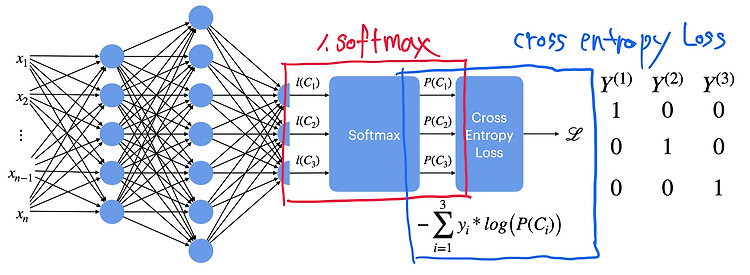
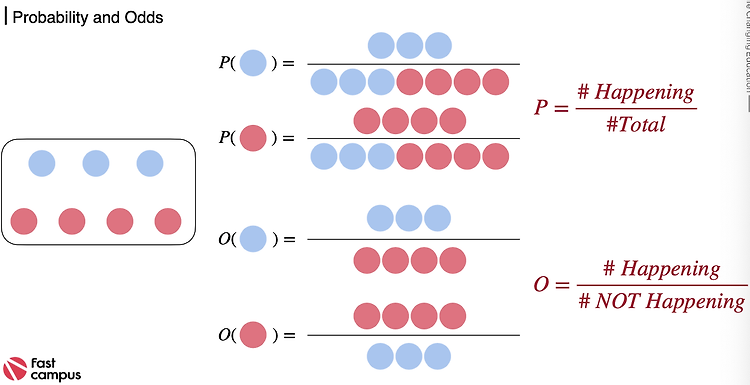
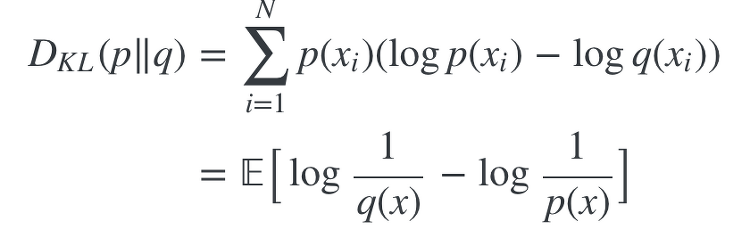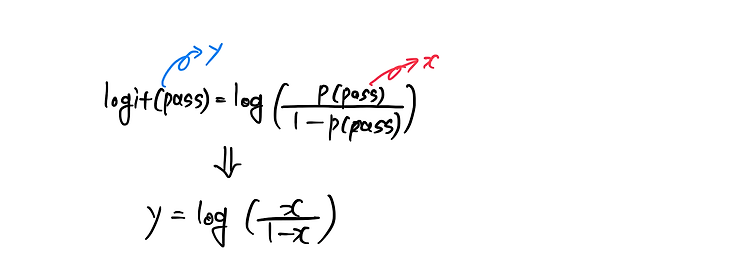로지스틱회귀를 위한 범주형 데이터를 만드는 방법 import numpy as np x_dict={'mean':1, 'std':1, 'n_sample':300, 'noise_factor':0.3,'cutoff':1, 'direction':1} def dataset_generator(x_dict): x_data=np.random.normal(x_dict['mean'], x_dict['std'], x_dict['n_sample']) #np.random.normal(평균,표준편차,갯수) : 평균과 표준편차에 맞는 데이터를 갯수만큼 랜덤으로 만든다 x_data_noise=x_data+x_dict['noise_factor']*np.random.normal(0,1,x_dict['n_sample']) # 반목문 필요없..

1. 개요 내가 만든 모듈을 import해서 쓰는 방법이다. 같은 디렉토리안에 넣고, a.py모듈을 b.py에서 쓰고싶으면 b.py에서 import a를 하면된다. 즉 아래와 같이 쓸 수 있다. # b.py파일 import a 2. 예시 - 디렉토리 구성 basic_nodes라는 모듈을 만들고, 이를 test2에서 불러 오려고 한다. 디렉토리 구성은 아래와 같다. - basic_node.py import numpy as np class mean_node: def __init__(self): self._x=None self._z=None def forward(self, x): self._x = x self._z = np.mean(self._x) return self._z def backward(self, ..

1. 풀이 visit 리스트를 갱신을 queue에서 pop된 다음 해주면 된다. 그렇게 하면 x위치까지 최단시간에 도착하는 경로의 수 만큼 큐에서 pop이 된다. 그러니까 임의의 위치까지 가는 최단경로(최단시간)는 q에 계속 보존이 된다. 일반적인 bfs문제처럼 조건확인후 아래와 같이 visited[loc]==-1일때 visited[loc]=visited[loc+x]+1 하면 처음으로 찾은 최단경로 외에 다른 최단경로는 q에 안들어간다. 2. 소스코드 from collections import deque maxNum=100000 N,K=map(int,input().split()) visited=[-1 for i in range(maxNum+1)] q=deque([(N,0)]) case=0 T=maxNum..

time.sleep()이라는 함수를 이용해서 프로그램을 원하는 시간(초)동안 정지시킬 수 있다. import time print(time.time()) time.sleep(5) print(time.time()) 1603299754.9303198 1603299759.930472 Process finished with exit code 0 * time.time() : 1970년 1월 1일 0시 0분 0초 부터 경과한 시간(초). 현재도 계속 흐르고 있다.

1. x값에 따른 loss function의 모양 loss function의 식은 아래와 같다. y값이 1일때 x값에 따른 loss function의 모양은 아래와 같다. 2. loss function을 이용하여 cost function 시각화 loss function의 식은 아래와 같다. 즉 cost function은 loss function의 합이므로 3차원으로 나타내면 아래와 같아진다. 여러개의 값일때는 아래와 같아진다. *출처 : 패스트캠퍼스 수학적으로 접근하는 딥러닝 올인원패키지 신경식강사

1. 풀이 영어 문제이지만 알고리즘분류와 input만 봐도 뭘구해야 하는지 알 수 있다. 점수가 최대가 되는 route를 찾는 문제이므로 point간 점수에 -1을 곱해준 뒤 최단거리를 찾으면 된다. 이때 시작점과 종료지점이 모든점이 될 수 있기 때문에 플로이드로 모든 정점들 사이의 거리를 구해주고 그중 가장 작은 값을 구해준다 (그다음 -1을 곱해준다) 추가로 이 문제를 통해 플로이드 문제를 풀 때 해야하는 작업들을 정리한다 2. 플로이드 와샬 구현 딱 세가지만 기억!!!!!! (1) 초기값을 +무한대로 초기화 한다. - 최단거리를 찾는 문제이다. 시작점을 제외한 모든점들은 당연히 +무한대로 초기화한다. dist=[[INF for j in range(n)] for i in range(n)] (2) 자기..

위와같은 흐름에서 각각의 함수의 모양을 확인하고 학습되는 과정을 살펴본다. 1. 함수의 모양 ( 예시는 (x,y)=(1,1) 일때 ) (1) affine fuction - 식 - 그래프 (x=1일때 함수의 그래프는 아래와 같다. z축의 의미는 z^i이다.) (2) activation function (logistic function) - 식 - 그래프 (x=1일때 함수의 그래프는 아래와 같다. z축의 의미는 y^i이다.) (3) loss function (binary cross entropy) - 식 - 그래프 (z축의 의미는 Loss) 2. loss의 의미 (1) 위치별 prediction 값 실제값이 1인데 예측값이 1에 가까우면 loss는 낮아 하고 예측값이 0에 가까우면 loss는 높아야 한다. ..

1. coefficient의 부호에 따른 모양 (1) 양수일때 양수일때는 우상 그래프가 만들어진다 a가 클수록 점점더 경사가 가팔라 진다 a가 커질수록 보라색 ->붉은색 이 된다. (2) 음수일때 음수일때는 좌상그래프가 만들어진다 a가 작을수록 (절댓값은 클수록) 가팔라진다 a가 작아질수록 (절댓값은 커질수록) 보라색->빨간색이 된다. 2. bias의 부호에 따른 모양 (1) 양수일때 bias가 양수이면 왼쪽으로 이동한다. bias가 커질수록 왼쪽으로 이동한다. 즉 bias가 커질수록 보라색 -> 빨간색으로 이동한다. (2) 음수일때 bias가 음수이면 오른쪽으로 이동한다. bias가 작아질수록 오른쪽으로 이동한다. 즉 bias가 작아질수록 보라색 -> 빨간색으로 이동한다. 3. bias만 그래프의 이동..

1. forward propagation 2. backward propagation

파이썬에서 product라는 모듈을 이용하여 종복순열을 구현할 수 있다. 1. 모듈 불러오기 from itertools import product 2. 사용법 (1) 예시1 a=list(product([0,1,2],[0,1,2])) print(a) [(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)] (2) 예시2 *같은 모양은 repeat 파라미터를 이용할 수도 있다. a=list(product([0,1,2],repeat=2)) print(a) [(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)] (3) 예시3 a=list(product([0,1,2]..

1. softmax 마지막 output layer에는 아무런 활성함수를 넣지 않기 때문에 결과값이 -무한~+무한 을 가질 수 있다. 따라서 이를 logit으로 해석할 수 있고, softmax함수를 이용하여 확률의 형태로 바꿔줄 수 있다. 2. cross entropy 확률형태로 바뀐 결과값 p_ci를 y_i와 비교하여 loss를 측정한다. 이 loss가 바로 cross entropy loss이다. 이를 이용하여 back propagation을 진행하여 파라미터를 개선한다. * 출처 : 패스트캠퍼스 수학적으로 접근하는 딥러닝 올인원 패키지 Online.

binary entropy의 의미 및 정보이론적 해석을 다룬적이 있다. (sosoeasy.tistory.com/356) 그렇다면 더 나아가서 cross entropy가 무엇인지를 KL Divergence를 통해서 해석해 본다. 1. KL Divergence kl divergence는 정보량의 차이에 대한 기댓값이다. 즉 kl divergence를 그래프로 나타내면 아래와 같다. 2. KL Divergence를 이용한 cross entropy의 해석 kl divergence를 변형하면 cross entropy에 대한 식으로 정리된다. 그리고 이를 cross entropy에 대해서 정리하면 아래와 같아진다. 즉 cross entropy를 최소화하는것은 kl divergence를 최소화 하는것과 같은 것이다...

1. 정보량 (1) 확률과 반비례 관계 발생할 확률이 낮은 사건이 발생한다는 사실을 알때 정보의 양은 커진다. 그러니까 확률과 정보의 양은 반비례하다. (2) 숫자 예시 1~100까지 숫자중 정답인 숫자를 맞춰야 하는 문제가 있다고 가정하자. 정답이 1~10까지 중에 있다는 정보는 확률이 10/100 => 정보의 양은 10 정답이 1~20까지 중에 있다는 정보는 확률이 20/100 -=> 정보의 양은 5 . . 정답이 1~100까지 중에 있다는 정보는 확률이 100/100 => 정보의 양은 1 (3) 로그취하기 이때 동전 던지기로 정보의 양은 표현하면 동전 하나를 던졌을때 하나가 앞면이 나올 확률은 1/2 => 정보의 양은 2 동전 두개를 던졌을 때 두개가 앞면이 나올 확률은 1/2^2 => 정보의 양은..

그냥 하라는대로 하면 되는문제인데 인덱스 장난이 심한 문제. 그래서 코딩에서 가장 중요한건 차분히 침착하게 푸는것 이라는것을 다시한번 상기시키는 문제. 침착해 침착해 from copy import deepcopy N=int(input()) P=list(map(int,input().split())) S=list(map(int,input().split())) #카드덱 dq=[i for i in range(N)] #현재 플레이어상태 player=[[] for i in range(3)] for i in range(N): p=i%3 player[p].append(i) ini=deepcopy(player) #목표값 target=[[] for i in range(3)] for i in range(N): target[..

0. 서론확률을 input으로 받았을 때 적절한 y값을만들어 주는 logit function에 대해서 알아보았다(sosoeasy.tistory.com/352)그렇다면 logit값을 입력으로 받았을 때 이를 확률로 바꿔주는 sigmoid(label이 3개이상일때는 softmax)에 대해서 알아본다. 1. logit의 함수는 아래와 같다 2. logit 함수로 부터 sigmoid함수를 역함수 형태로 유도할 수 있다 즉 각각의 함수의 역할은 다음과 같다 3. softmax는 여러 lable이 있을때 쓰는 활성함수. 분모가 달라진다 4. DNN에서의 흐름output layer의 결과값을 logit으로 생각하면, 이 logit을 sigmoid( softmax )함수에 적용하면 결과값으로 확률이 나온다. * 출처 ..

1. 풀이 제일왼쪽열, 제일 위쪽 행의 값이 주어지고, 다른 자리는 왼,왼위,위 중 가장 큰 수가 들어오면 되는 조건을 보면 아래와 같은 점화식이 만들어진다. L[i][j]=max(L[i-1][j],L[i-1][j-1],L[i][j-1]) 위의 점화식을 만든것 만으로 뭔가 대단한걸 생각해낸 것 같아서 정답인줄 알았지만 시간초과이다. (N=1,000,000) 핵심은 주어지는 왼쪽열, 위쪽행의 값들이 순차적으로 커진다는 것이다. 즉 점화식의 결과는 반드시 아래와 같아진다는 것이다. max(L[i-1][j],L[i-1][j-1],L[i][j-1])=L[i-1][j] 그러니까 0열을 제외한, 즉 1열보다 뒤에 있는 모든 행들은 0행의 값들을 그대로 받을 수 밖에 없다. 따라서 0열과 0행을 다 누적해서 더해주고..

1. odd와 probability의 차이 2. odd를 확률로 나타내기 3. odd의 문제 odd는 0이상의 값을 가질 수 있는데, 비율이 좋지 않다. 4. logit 따라서 log를 붙여준다. 즉 logit(pass)=log(o(pass))=log(p(pass)/(1-p(pass))=log(p(pass))-log(1-p(pass)) * 출처 : 패스트캠퍼스 수학적으로 접근하는 딥러닝 올인원 패키지 Online.

0. 설명 로지스틱회귀에서 사용하는 loss function인 binary cross entropy가 어떻게 만들어졌는지 살펴본다 1. loss function의 의미 loss function은 우리가 원하는값이 나오면 작은값이 나와야 하고, 우리가 원하지 않은 값이 나오면 커야 한다. 즉 결과값이 0이 나와야 하는데 1이나오면 loss는 커져야 하고, 0이 나오면 loss는 작아져야 한다. 이를 식으로 나타내면 아래와 같다. 2. log함수 그런 역할을 해주는 식이 log함수이다. 식은 아래와 같다 즉 label이 0이면 0에 가까워질수록 작아지고, 1에 가까워질수록 커지는 -log(1-x)를 loss function으로 쓰고 label이 1이면 1에가까워질수록 작아지고, 0에 가까워질수록 커지는 -l..