
위와같은 흐름에서 각각의 함수의 모양을 확인하고 학습되는 과정을 살펴본다.
1. 함수의 모양 ( 예시는 (x,y)=(1,1) 일때 )
(1) affine fuction
- 식

- 그래프 (x=1일때 함수의 그래프는 아래와 같다. z축의 의미는 z^i이다.)
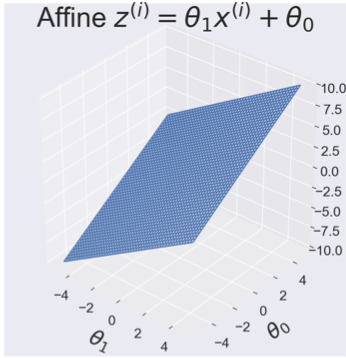
(2) activation function (logistic function)
- 식

- 그래프 (x=1일때 함수의 그래프는 아래와 같다. z축의 의미는 y^i이다.)

(3) loss function (binary cross entropy)
- 식

- 그래프 (z축의 의미는 Loss)

2. loss의 의미
(1) 위치별 prediction 값

실제값이 1인데 예측값이 1에 가까우면 loss는 낮아 하고 예측값이 0에 가까우면 loss는 높아야 한다.
따라서 위 사진에서 0에 가까운 파란색부분은 실제값이 1이기 때문에 loss가 높고 1에 가까운 빨간색 부분은 loss가 낮다.
이를 2차원으로 시각화 하면 아래와 같다.

(2) 왜 빨간색 부분이 sigmoid function에서 1에 가까운가?
시그모이드 함수에서 세타0과 세타1의 변화에 따른 결과값이 아래와 같이 나온다.

즉 세타0과 세타1이 커질 수록 예측값은 1에 가까워지기 때문에 loss는 0에 가까워지고,
세타0과 세타1이 작아질 수록 예측값은 0에 가까워지기 때문에 loss는 1에 가까워진다.
3. 학습과정
학습은 loss가 낮아지는 형태로 진행이 된다(back propagation).
이를 그래프에서 표현하면 아래와 같고

2차원으로 시각화된 그래프에서 표현하면 아래와 같다.

* 출처 : 패스트캠퍼스 수학적으로 접근하는 딥러닝 올인원 패키지 Online.
