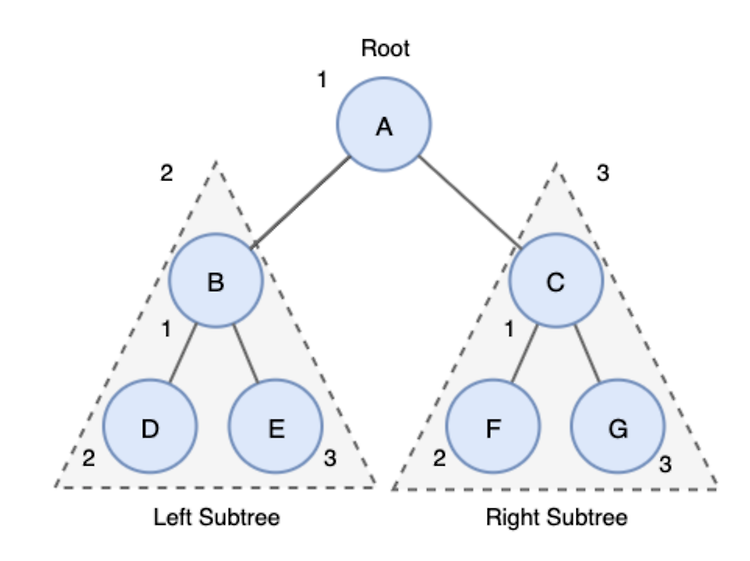
트리순회 트리를 순회할 때 어떤 노드를 먼저 탐색하느냐에 따라 전위,중위,후위로 나눌 수 있다. 각각의 순회를 알아 본다. 전위순회 부모 -> 왼쪽자식 -> 오른쪽자식 더이상 부모노드가 없을때 그 다음 노드(왼쪽자식)을 탐색한다 중위순회 왼쪽자식 -> 부모 -> 오른쪽자식 더이상 왼쪽자식이 없을때 그다음 노드(부모)를 탐색한다 후위순회 왼쪽자식 -> 오른쪽자식 -> 부모 그다음 왼쪽자식이 없을때 그다음 노드(오른쪽자식)을 탐색한다 *출처 : https://hongku.tistory.com/160 예시코드 (백준 1991 트리순회) def preorder(N): global graph if N in graph: print(N, end="") preorder(graph[N][0]) preorder(graph..

1. 풀이 (1) 입력이 하나의 그래프임이 보장될때 트리일 조건은 (노드개수-1)==(간선개수)가 된다. (2) 간선개수가 0인것은 빈트리이므로 이것역시 트리이다. 2. 소스코드 #include #include #include #include using namespace std; int main() { int num1, num2; string ans; int t = 1; while (1) { cin >> num1 >> num2; if (num1 < 0) { break; } // test case else { vector graph; set s; // 입력 while (1) { if (num1 == 0 and num2 == 0) { break; } else { graph.push_back(make_pair..

1. 함수의 구성 유니온 파인드는 find와 union 두가지 함수로 구성이 된다. (1) find는 그래프에서 루트노드를 찾아주는 함수이다. int find(int x) { if (parent[x] == x) { return x; } else { return parent[x] = find(parent[x]); } } (2) union은 서로 연결되어 있지 않은 그래프를 연결시키는 함수이다. void Union(int x, int y){ x = find(x); y = find(y); if(x!=y){ parent[y] = x; } } 2. 함수의 사용 유니온 파인드는 아래의 두가지 경우에 사용할 수 있다. (1) 그래프가 연결되어 있는지 확인할 때 (ex [boj]1717_집합의 표현) 어떤 두 노드의 ..