정상성 테스트 및 비정상성 제거 실습

0. 정상성의 의미

 

정상성의 의미와 예시에 대해서 아래의 글에 정리했다.

sosoeasy.tistory.com/387

시계열에서 정상성의 의미

 

1. 정상화 및 정상성 테스트

이번 장에서는 비정상성 데이터를 정상화 하고, 정상성을 테스트 하는 방법에 대해서 실습해 본다.

정상화 하는 방법은 4가지 정도가 있다.

(1) 추세차분

(2) 계절성차분

(3) 로그화

(4) box-cox변환

각각을 실습을 통해 수행해 본다

 

2. (1)추세차분, (2)계절성 차분

비정상성을 없애기 위해선 추세, 계절성을 없애야 한다.

또한 정상성을 테스트하는 방법 중에는 ADF와 KPSS 가 대표적이다.

ADF는 추세가 제거 되었는지 확인하는데 유용하고, KPSS는 계절성 제거가 되었는지 확인하는데 유용하다.

아래의 실습에서 확인해 본다.

 

<example>

# 라이브러리 및 데이터 로딩
import pandas as pd
from statsmodels import datasets
import matplotlib.pyplot as plt
import statsmodels.api as sm
%reload_ext autoreload
%autoreload 2
from module import stationarity_adf_test, stationarity_kpss_test

raw_set = datasets.get_rdataset("deaths", package="MASS")
raw = raw_set.data

# 시간변수 추출
raw.time = pd.date_range('1974-01-01', periods=len(raw), freq='M')
raw['month'] = raw.time.dt.month

 

- 원데이터

# 데이터 확인 및 추세 추정
display(raw.tail())
plt.plot(raw.time, raw.value)
plt.show()

display(stationarity_adf_test(raw.value, []))
display(stationarity_kpss_test(raw.value, []))
sm.graphics.tsa.plot_acf(raw.value, lags=50, use_vlines=True, title='ACF') #자기상관계수
plt.tight_layout()
plt.show()

#c(month):더미화, -1:절편제거
result = sm.OLS.from_formula(formula='value ~ C(month) - 1', data=raw).fit() 
display(result.summary())

plt.plot(raw.time, raw.value, raw.time, result.fittedvalues)
plt.show()

 

 

원데이터 분포

정상성 탐색(왼쪽), 자기상관계수분석(오른쪽)

OLS회귀분석 결과(왼쪽,중간), 잔차분석(오른쪽)

원데이터와 회귀분석 결괏값

 

 

- 추세제거 데이터

# 추세 제거 및 정상성 확인
## 방법1
plt.plot(raw.time, result.resid)
plt.show()

display(stationarity_adf_test(result.resid, []))
display(stationarity_kpss_test(result.resid, []))
sm.graphics.tsa.plot_acf(result.resid, lags=50, use_vlines=True)
plt.tight_layout()
plt.show()

 

 

 

- 계절성 제거 데이터

# 계절성 제거 및 정상성 확인
## 방법2
sm.graphics.tsa.plot_acf(raw.value, lags=50, use_vlines=True)
plt.show()

plt.plot(raw.time, raw.value)
plt.title('Raw')
plt.show()
seasonal_lag = 3
plt.plot(raw.time[seasonal_lag:], raw.value.diff(seasonal_lag).dropna(), label='Lag{}'.format(seasonal_lag))
seasonal_lag = 6
plt.plot(raw.time[seasonal_lag:], raw.value.diff(seasonal_lag).dropna(), label='Lag{}'.format(seasonal_lag))
seasonal_lag = 12
plt.plot(raw.time[seasonal_lag:], raw.value.diff(seasonal_lag).dropna(), label='Lag{}'.format(seasonal_lag))
plt.title('Lagged')
plt.legend()
plt.show()

seasonal_lag = 6
display(stationarity_adf_test(raw.value.diff(seasonal_lag).dropna(), []))
display(stationarity_kpss_test(raw.value.diff(seasonal_lag).dropna(), []))
sm.graphics.tsa.plot_acf(raw.value.diff(seasonal_lag).dropna(), lags=50, 
                         use_vlines=True, title='ACF of Lag{}'.format(seasonal_lag))
plt.tight_layout()
plt.show()

seasonal_lag = 12
display(stationarity_adf_test(raw.value.diff(seasonal_lag).dropna(), []))
display(stationarity_kpss_test(raw.value.diff(seasonal_lag).dropna(), []))
sm.graphics.tsa.plot_acf(raw.value.diff(seasonal_lag).dropna(), lags=50, 
                         use_vlines=True, title='ACF of Lag{}'.format(seasonal_lag))
plt.tight_layout()
plt.show()

 

 

lag6의 정상성테스트 및 자기상관 결과

lag12의 정상성테스트 및 자기상관 결과

 

 

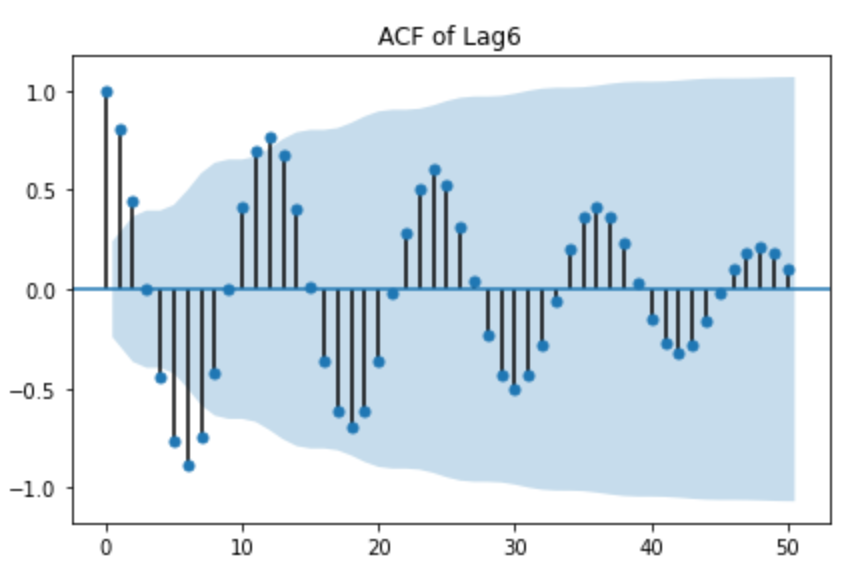
p-value	Raw-data	추세제거	계절성제거(lag6)	계절성제거(lag12)
adf(유의수준보다 작으면 정상)	0.88	0	0	0.23	=> 추세가 제거되면 정상이라고 판단
kpss(유의수준보다 크면 정상)	0.02	0.03	0.1	0.1	=> 계절성이 제거되면 정상이라고 판단
acf(그래프로 계절성 여부 확인)	계절성있어보임	없어보임	있어보임	없어보임

 

결론 => lag 12를 사용하는것이 좋아보임

 

3. (3)로그화

# 라이브러리 호출
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
%reload_ext autoreload
%autoreload 2
from module import stationarity_adf_test, stationarity_kpss_test

# 데이터 준비
data = sm.datasets.get_rdataset("AirPassengers")
raw = data.data.copy()

# 데이터 전처리
## 시간 인덱싱
if 'time' in raw.columns:
    raw.index = pd.date_range(start='1/1/1949', periods=len(raw['time']), freq='M')
    del raw['time']

## 정상성 확보
plt.figure(figsize=(12,8))
raw.plot(ax=plt.subplot(221), title='Y', legend=False)
np.log(raw).plot(ax=plt.subplot(222), title='log(Y)', legend=False)
raw.diff(1).plot(ax=plt.subplot(223), title='diff1(Y)', legend=False)
np.log(raw).diff(1).plot(ax=plt.subplot(224), title='diff1(log(Y))', legend=False)
plt.show()

 

로그를 한후 가 더 정상성이 높아 보인다. (차분시에도 마찬가지)

 

 

4. (4)box-cox

box-cox변환 : 정규분포가 아닌 자료를 정규분포를 만들기 위해 사용

# 라이브러리 호출
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
import scipy as sp
%reload_ext autoreload
%autoreload 2
from module import stationarity_adf_test, stationarity_kpss_test

# 데이터 준비
data = sm.datasets.get_rdataset("AirPassengers")
raw = data.data.copy()


# Box-Cox 변환 모수 추정
# 정규분포의 특정 범위(x)에서 lambda를 바꿔가며 정규성(measure:y)이 가장 높은 lambda(l_opt)를 선정
x, y = sp.stats.boxcox_normplot(raw.value, la=-3, lb=3)
y_transfer, l_opt = sp.stats.boxcox(raw.value)
print('Optimal Lambda: ', l_opt)

plt.plot(x, y)
plt.axvline(x=l_opt, color='r', ls="--")
plt.tight_layout()
plt.show()

plt.figure(figsize=(12,4))
sm.qqplot(raw.value, fit=True, line='45', ax=plt.subplot(131))
plt.title('Y')
sm.qqplot(np.log(raw.value), fit=True, line='45', ax=plt.subplot(132))
plt.title('Log(Y)')
sm.qqplot(y_transfer, fit=True, line='45', ax=plt.subplot(133))
plt.title('BoxCox(Y)')
plt.tight_layout()
plt.show()

 

 

 

 

*출처 : 패스트캠퍼스 "파이썬을 활용한 시계열 데이터분석 A-Z"