0. 정규화 선형회귀?
(1) 선형회귀 계수(Weight)에 대한 제약 조건을 추가함으로써 모형이 과도하게 최적화되는 현상인 과최적화를 막는 방법
(2) 계수의 크기가 커지면 과적합됨. => 계수의 크기를 제한함
* 기존의 회귀분석?
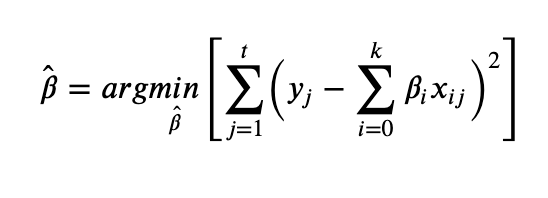
1. 릿지회귀(ridge Regression)
(1) 정의
추정계수의 제곱합을 최소로 하는것.

(2) 특징
- 제곱합을 최소화 하기 때문에 계수의 크가 줄어듬 => 과적합이 방지됨
- 다중공선성이 분산되기 때문에 효과적
- 딥러닝 loss function에서 L2 panelty로 사용됨
(3) 코드
# Ridge
fit = Ridge(alpha=0.5, fit_intercept=True, normalize=True, random_state=123).fit(X_train, Y_train)
pred_tr = fit.predict(X_train)
pred_te = fit.predict(X_test)
<exmaple>
import warnings
warnings.filterwarnings('always')
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge, Lasso, ElasticNetdiabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target
print('Data View')
display(pd.concat([pd.DataFrame(y, columns=['diabetes_value']), pd.DataFrame(X, columns=diabetes.feature_names)], axis=1).head())
alpha_weight = 0.5
fit = Ridge(alpha=alpha_weight, fit_intercept=True, normalize=True, random_state=123).fit(X, y)
pd.DataFrame(np.hstack([fit.intercept_, fit.coef_]), columns=['alpha = {}'.format(alpha_weight)])
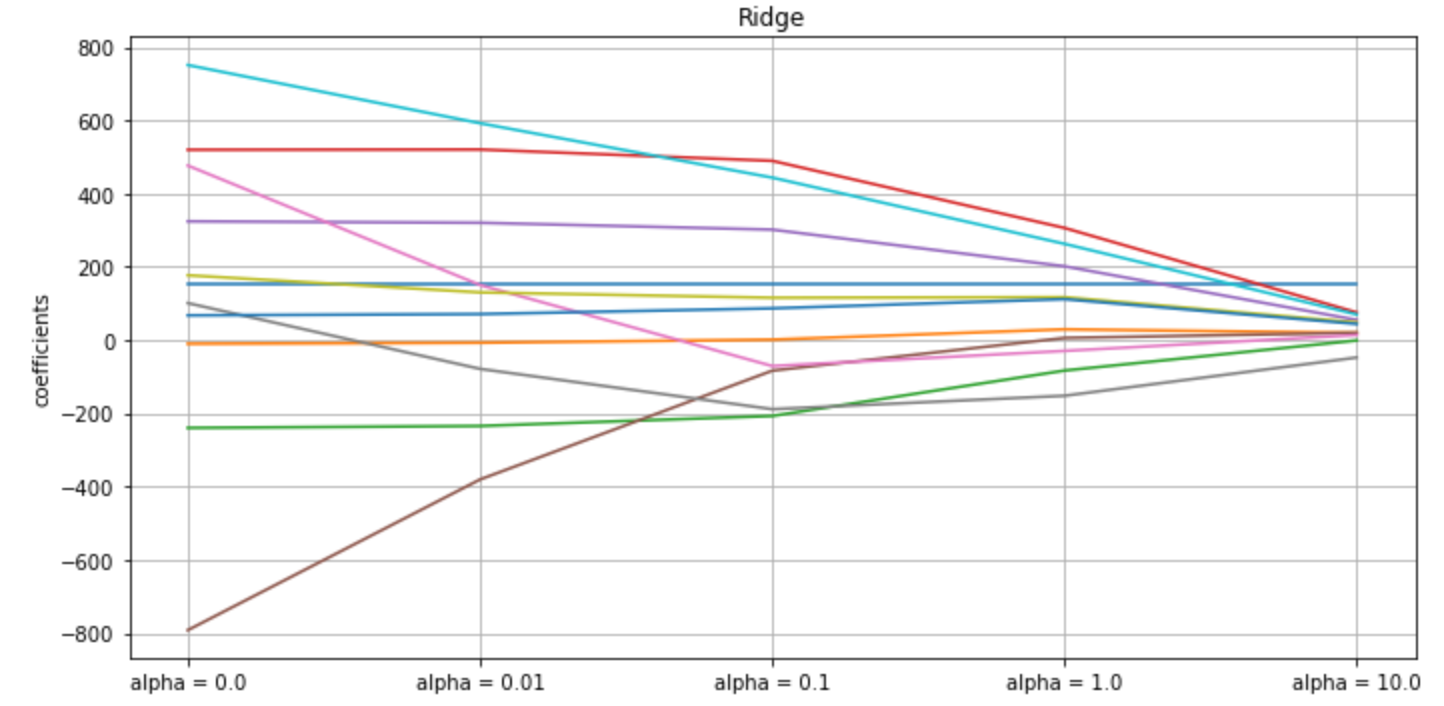
(4) 추정제곱가중치의 변화(각기 다른 색깔)에 따른 각 컬럼의 계수

2. 라쏘회귀(lasso Regression)
(1) 정의
LASSO(Least Absolute Shrinkage and Selection Operator)
추정계수의 절댓값 합을 최소로 하는것 (0에 가까워짐)
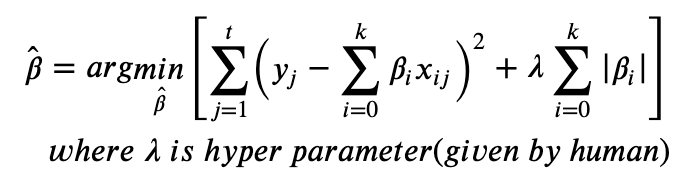
(2) 특징
- 몇몇 기여도가 낮은 계수들이 0으로 수렴하려고 함
- 반면 기여도가 높은 특정변수의 계수는 커지는 단점이 있음
- 딥러닝 loss function에서 L1 panelty로 사용됨
(3) 코드
# LASSO
fit = Lasso(alpha=0.5, fit_intercept=True, normalize=True, random_state=123).fit(X_train, Y_train)
pred_tr = fit.predict(X_train)
pred_te = fit.predict(X_test)
<exmaple>
import warnings
warnings.filterwarnings('always')
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge, Lasso, ElasticNetdiabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target
print('Data View')
display(pd.concat([pd.DataFrame(y, columns=['diabetes_value']), pd.DataFrame(X, columns=diabetes.feature_names)], axis=1).head())
alpha_weight = 0.5
fit = Lasso(alpha=alpha_weight, fit_intercept=True, normalize=True, random_state=123).fit(X, y)
pd.DataFrame(np.hstack([fit.intercept_, fit.coef_]), columns=['alpha = {}'.format(alpha_weight)])
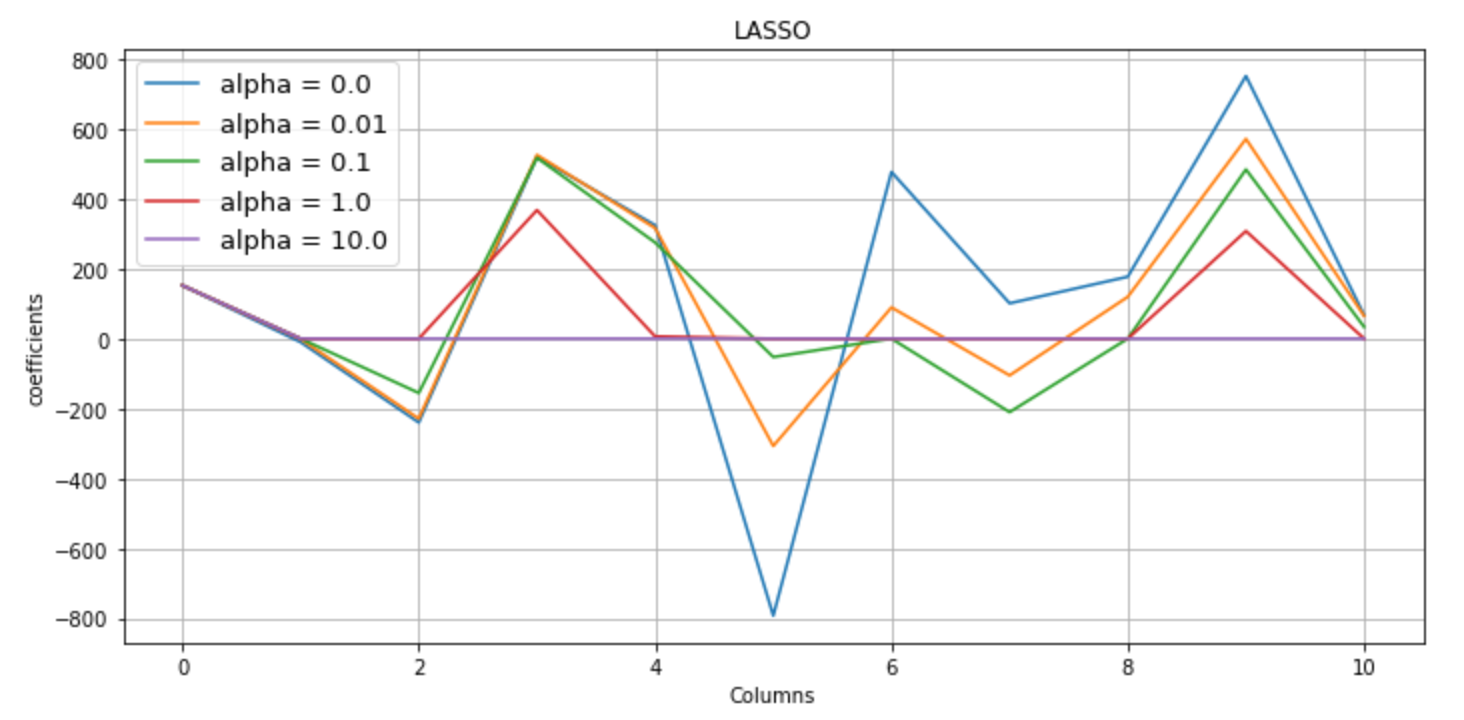
(4) 추정절대가중치별(각기다른 색깔의 그래프) 각 컬럼의 계수에 대한 그래프
- 0으로 수렴하는 계수가 존재한다

3. 엘라스틱 넷(elastic net)
(1) 정의
추정계수의 절댓값 합과 제곱합을 동시에 최소로 하는것
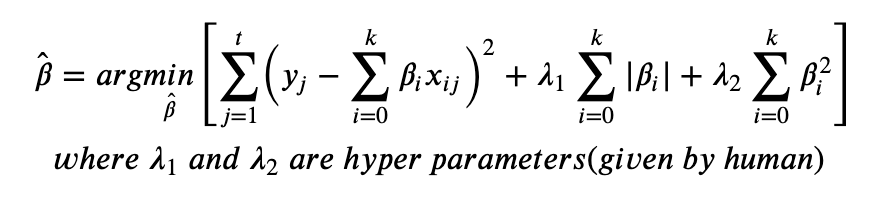
(2) 특징
큰 데이터셋에서 릿지와 라쏘의 효과를 모두 반영하기 좋음 (적은 데이터셋은 효과적음, 릿지 라쏘와 반대)
(3) 코드
# Elastic Net
fit = ElasticNet(alpha=0.01, l1_ratio=1, fit_intercept=True, normalize=True, random_state=123).fit(X_train, Y_train)
pred_tr = fit.predict(X_train)
pred_te = fit.predict(X_test)
*출처 : 패스트캠퍼스 "파이썬을 활용한 시계열 데이터분석 A-Z"
