회귀분석에서 조건수(Condition Number)

1. 식

 

2. 의미

변수들간에 상관성을 나타낸다.

조건수가 낮다 => 변수들이 서로 독립이다 => 오버피팅 할 확률이 낮다. => 오차에 강건하다

조건수가 높다 => 변수들이 서로 상관성이 많다 => 오버피팅 할 확률이 높다. => 오차에 민감하다

 

3. 예시

yi=c1x1i+c2x2i 

x1 = {1, 2, 3, 4}

x2 = {10, 20, 30, 40}

위와 같은 상황에서 x1과 x2는 상당히 높은 연관성이 있다.

따라서 조건수를 계산하면 높은값이 나온다.

또한 y값을 결정하는데 x1과 x2의 비슷한 추세가 크게 작용하여 이러한 형태에 대해서만 오버피팅하게 된다.

 

4. 오차의 영향

(1) 변수가 완전히 독립일때 - 오차에 강건함

# 조건수가 작을 때
# X 데이터
import numpy as np
A = np.eye(4)
A

 

# Y 데이터
Y = np.ones(4)

 

# 계수 추정
# 행렬곱
np.linalg.solve(A, Y)

 

# X 데이터 오차반영
A_new = A + 0.0001 * np.eye(4)
A_new

 

# 계수 추정
np.linalg.solve(A_new, Y)

 

# 조건수 확인
np.linalg.cond(A)

# 컨디션넘버가 1? => 모든데이터가 완전히 독립임 => 오차에 로버스트하다

 

(2) 변수가 종속적일때 - 오차에 민감함

# 조건수가 클 때
# X 데이터
# hilbert : 임의의 데이터
from scipy.linalg import hilbert
A = hilbert(4)
A

 

# Y 데이터
Y = np.ones(4)
Y

 

# 계수 추정
np.linalg.solve(A, Y)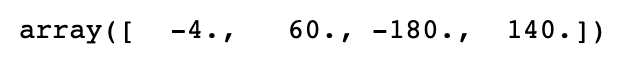

 

# X 데이터 오차반영
A_new = A + 0.0001 * np.eye(4)
A_new

 

# 계수 추정
# 조금의 오차로 인해 큰 차이가 생긴다.
np.linalg.solve(A_new, Y)

 

# 조건수 확인
np.linalg.cond(A)

# 컨디션넘버가 매우크다? =>  오차에 민감하다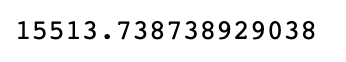

 

5. 조건수 감소 방법

(1) 스케일링(scaling) : 변수들의 단위차이로 숫자의 스케일이 다른경우.

(2) 차원축소 (VIF, PCA) : 독립변수들 간에 상관관계가 높은 "다중공선성" 존재할 경우

(3) 정규화(Resularization) : 독립변수간 의존성이 높은 변수들에 패널티를 부여하는 정규화

 

* 출처 : 패스트캠퍼스 파이썬을 활용한 시계열 데이터분석 A-Z